一切源于一个疑问,为什么傅里叶正变换表达式中将时域信号f乘上虚指数因子再积分就能转换为频域呢?
第一直觉便是欧拉公式,合适的时域信号可以转换为一系列不同频率的余弦信号,欧拉公式恰好是连接指数与三角函数的桥梁,隐隐约约的在公式里体现了它转换的内涵。但是这一个虚指数因子到底是怎么运作的呢?
假设现在有一个频率为3的余弦信号,1s振动3次,如果我用旋转矢量图来表示余弦信号的幅值[0,2A],矢量长度代表余弦信号幅值大小。旋转矢量每2s转一圈,那么图中大概可以看出是画了六个花瓣(对应2s内信号的六个幅值);倘若旋转矢量每1/3s转一圈,即1秒3圈,那么图中只有一个花瓣。
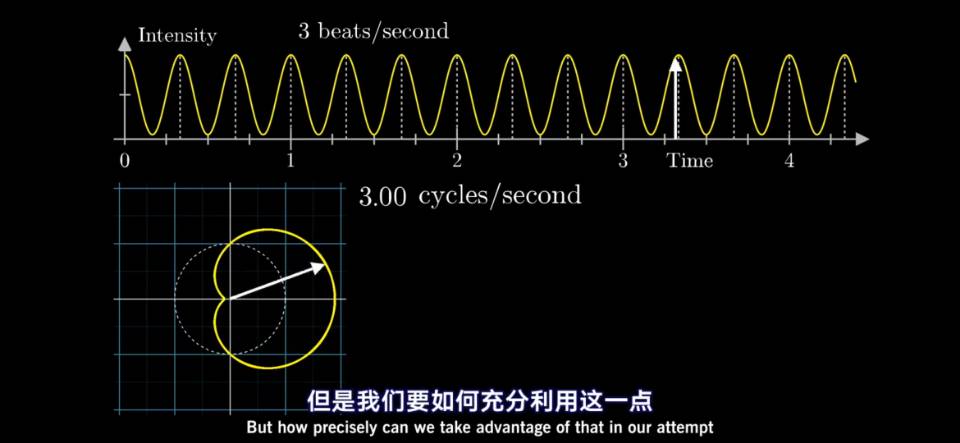
恰好旋转矢量的旋转频率正是对应着余弦信号的频率。真的是巧合吗?
随着旋转矢量的转速发生变化,花瓣数量也在变化,但画出的图像也会有混沌的时刻,当达到信号频率的时候就会变得有规律。如果我们能找到一种描述图形规律性的办法,就能找出我们需要的旋转频率。这里我们吧图形看作一个有质量的物体,存在重心(如下图红点)。当图形混沌的时候,重心总是接近于原点;而当其规律的时候,重心将会相对偏移原点很多。如果我们把重心离原点的距离向量与旋转频率联系起来,画出二维函数图,就能找到我们所要的频率。
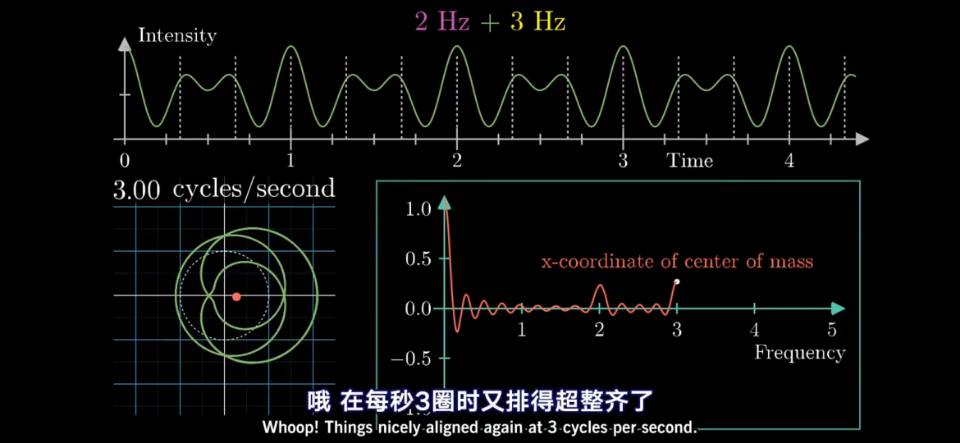
回顾一下,我们引入了旋转矢量和重心向量的观点,从另一个角度找到了分解信号频率的方法。那么,这跟虚指数因子有什么关系呢?
在描述重心向量的时候,它总是绕着原点旋转移动,而复平面恰好是一个适合描述旋转的二维平面。利用欧拉恒等式,恰好可以用虚指数因子来表示出向量的旋转。
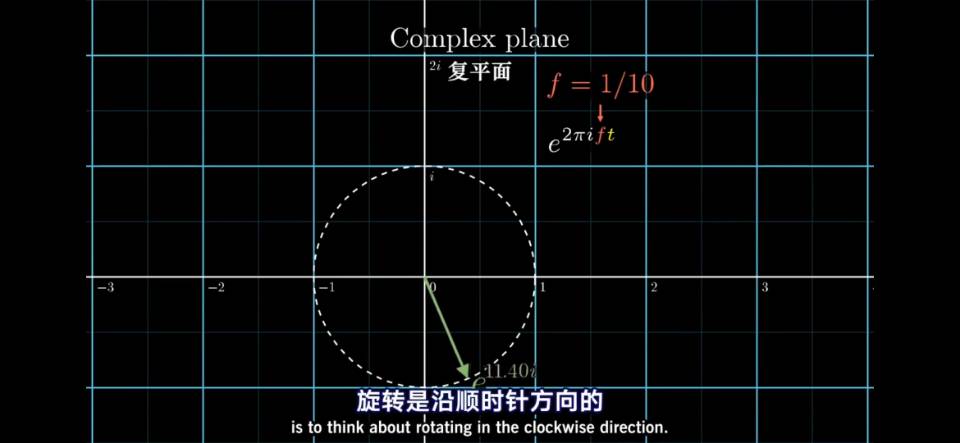
为什么能用指数因子来表示复平面上的旋转呢?欧拉公式可以知道,指数展开后实部为余弦函数,虚部为正弦函数,在同一时间上,正余弦函数的幅值之和恒等于1,真好在复平面上画出一个单位圆,怪不得说欧拉公式是最美丽的公式。而指数的幂中i的系数恰好体现了它的旋转速度,如果系数是ω,根据欧拉公式它也可以体现三角函数的频率,于是我们把信号频率–旋转矢量转速–三角函数频率连接了起来,所用到的正是这个虚指数因子。
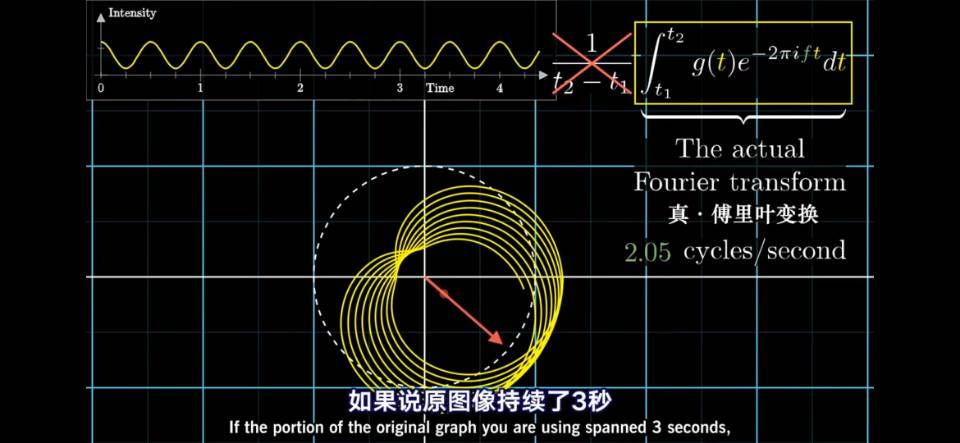
到此为止,正是从复平面描述旋转的角度进行观察,理解了傅里叶变换的实质。
数学太奇妙了,感谢3蓝1棕

